[ML Engineer 지식 공부] 기본지식 공부해보기 [1]

이번 포스팅에서는 제가 자주 찾아보는 카일스쿨 https://zzsza.github.io/data/2018/02/17/datascience-interivew-questions/ 블로그에서 나온 면접 질문들에 해당하는 내용에 대해서 공부해보고 정리를 해서 남겨두려고 합니다.

처음에는 다 알고 있다고 생각했는데 얼핏 알기만 하고 막상 누가 물어보면 대답을 제대로 할 수 없을 것 같은 것들이 많아서 블로그로 정리하면서 공부를해야겠다는 생각이 들어서 포스팅을 하게 되었네요.

같이 공부하고 댓글로 틀린 것들이 있으면 남겨주시면 좋겠습니다 :)

통계 및 수학

고유값(eigen value)와 고유벡터(eigen vector)에 대해 설명해주세요. 그리고 왜 중요할까요?
- LDA ?
  - 클래스를 가장 잘 구분할 수 있는 새로운 축을 찾아주기 위함
  - 두 클래스간 중심간의 거리 / 각 클래스 내 분산의 합 "
    - 따라서 수식은 다음과 같아지며 분모인 분산값은 최소화시킬수록, 분자인 거리값은 최대가 될수록 가장 잘 분류할 수 있는 축을 구하기 위한 목적함수가 정의된다.
    - 각 클래스의 중심에 데이터가 몰려있음을 가정하므로 '비선형 분포 데이터'에는 부적합하다.

- - LDA는 분류할 수 있게 분별 기준을 최대한 유지하며 축을 설정한다. 이게 PCA와는 다른 점이다.
  - LDA는 빨간점과 파란점들을 분류해내야 하는 목적을 갖고, 모이되 둘이 떨어지도록 축(화살표)을 좌상향으로 설정했다.
- PCA ?
  - Unsupervised learning의 일종
  - PCA는 보통 데이터의 분포에 대한 주성분 즉, 최적의 Feature 조합을 찾기 위한 방법이다. 여기서 주성분이란, 우리가 앞서 2.Eigen Value Decomposition 목차에서 배웠던 것을 적용하여 일명 '새로운 축(관점)'으로 데이터를 바라보는 것이다. 이렇게 PCA를 하는 목적을 최적의 Feature를 선택한다고 해서 'Feature Selection' 라 하거나 n개의 Feature를 n-1개이하의 Feature로 감소시킨다고 하여 'Feature Dimension Reduction' 이라고도 한다.
  - 데이터의 변동성이 가장 큰 방향으로 축을 설정해 데이터를 표현한다.
  - 알고리즘은 축소하고자 하는 데이터 간의 공분산행렬을 구하고 고유벡터를 추출해 PCA값을 산출하는 역할을 해준다.
  - PCA는 Eigen value decomposition(고유값 분할)을 통해 새로 만든 '축(관점)'으로 데이터를 바라보는 것이다.
  - 데이터들의 평균(중심)으로 원점을 가정한다. 그리고 Eigen value Decomposition을 통해서 공분산행렬, 고유값, 고유벡터를 구하게 됬다. 이렇게 고유값 분할을 통해 얻게 된 새로운 다양한 축(고유벡터) 관점에서 가장 큰 분산을 가질 때의 축을 기준으로 데이터를 바라보게 되는 것이다.
- https://data101.oopy.io/easy-understand-pca-lda
행렬계수(Rank)
- Column Rank : 선형독립인 열 벡터의 개수
- Row Rank : 선형독립인 행 벡터의 개수
- https://techblog-history-younghunjo1.tistory.com/66
샘플링(Sampling)과 리샘플링(Resampling)에 대해 설명해주세요. 리샘플링은 무슨 장점이 있을까요 [1] ?
- 샘플링은 모집단에서 임의의 Sampling을 뽑아내는 것으로, 쉽게 말해 표본 추출을 의미한다. 샘플링을 하는 가장 큰 이유는 모집단 전체에 대한 조사는 사실상 불가능하기 때문에 Sampling을 이용하여 모집단에 대한 추론을 하게 되는 것이다. 주로 머신러닝과 통계분야에서 흔히 볼 수 있으며 신뢰구간, 오버피팅, 분산 등 밀접한 관련이 있다. (모집단 -> 부분집단)
- 리샘플링은 내가 가지고 있는 샘플에서 다시 샘플 부분집합을 뽑아서 통계량의 변동성을 확인하는 것을 이야기한다. 즉, 같은 샘플을 여러 번 사용해서 성능 측정하는 방식이다. 가장 많이 사용되는 방법이며 종류로는 k겹 교차 검증 (k-fold cross validation), 부트스트래핑 (Out of Bag)이 있다. (부분집단 -> 부분집단)
확률 모형과 확률 변수는 무엇일까요?
- 확률변수는 확률로 표현하기 위한 event를 정의하는 것입니다.
- 확률이 정의된 Sample space 내에서, 이러한 확률변수를 0과 1사이의 확률로 mapping하는 함수를 확률 함수(확률 분포 함수)라고 합니다
  - 확률분포를 안다고 함은 확률분포를 나타내는 확률분포함수를 안다는 것이고, 확률분포함수를 안다는 것은 함수식을 구성하는 parameter를 안다는 것입니다.
- 확률 모형은 분포 함수(distribution function) 또는 밀도 함수(density function)라고 불리우는 미리 정해진 함수의 수식을 사용하여 분포의 모양을 정의(define)하는 방법이다. 이 때 분포의 모양을 결정하는 함수의 계수를 분포의 모수(parameter)라고 부른다.
누적 분포 함수와 확률 밀도 함수는 무엇일까요? 수식과 함께 표현해주세요
- 누적 확률 분포 함수 (cdf) 확률 변수 X가 - inf에서 x 이내에 존재할 확률
- 누적 밀도 함수의 단점 중의 하나는 어떤 값이 더 자주 나오든가 혹은 더 가능성이 높은지에 대한 정보를 알기 힘들다는 점이다 why? 확률변수 X 가 특정 값 이내에 등장할 확률이므로 일일히 계산해야하는 문제가 존재.
  - 확률 변수가 나올 수 있는 전체 구간 (-∞ ~ ∞)을 아주 작은 폭을 가지는 구간들로 나눈 다음 각 구간의 확률을 살펴보는 것
  - 이 때 사용할 수 있는 수학적 방법이 바로 미분(differentiation)으로 미분은 함수의 구간을 무한대 갯수로 쪼개어 각 구간 변화의 정도 즉, 기울기를 계산하는 방법
  - 누적 밀도 함수를 미분하여 나온 도함수(derivative)를 확률 밀도 함수(probability density function)라고 한다.
베르누이 분포 / 이항 분포 / 카테고리 분포 / 다항 분포 / 가우시안 정규 분포 / t 분포 / 카이제곱 분포 / F 분포 / 베타 분포 / 감마 분포 / 디리클레 분포에 대해 설명해주세요. 혹시 연관된 분포가 있다면 연관 관계를 설명해주세요 [2]
- 베르누이 분포
  - 결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행(Bernoulli trial).
  - 베르누이 시행의 결과를 실수 0 또는 1로 바꾼 것을 베르누이 확률변수(Bernoulli random variable)라고 한다. 베르누이 확률변수는 두 값 중 하나만 가질 수 있으므로 이산확률변수(discrete random variable)다.
  - 성공률이 p인 실험에서 성공이면 X = 1, 실패이면 X = 0이라 할 때, 확률변수 X의 확률분포를 모수 p인 베르누이 분포
  - 베르누이 분포는 매 시행마다 오직 두 가지의 가능한 결과만 가능한 확률 변수 X가 있을 때, 이러한 실험을 1회 시행하여 일어난 두 가지 결과에 의해 그 값이 각각 0과 1로 결정되는 확률변수 X가 따르는 분포
- 이항 분포
  - 성공확률이 $p$ 인 베르누이시행을 $n$ 번 반복시행할 때 성공횟수를 나타내는 확률변수 $X$ 의 분포를 이항분포
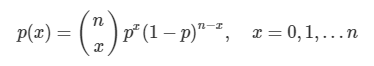
  - 매회 성공률이 p인 베르누이 실험을 독립적으로 n 번 반복할 때, 성공한 횟수(X)의 확률분포를 모수 n과 p인 이항 분포라 함.
  - X ~ B(n, p)로 나타냄.
- 카테고리 분포
  - 매 시행마다 K 개의 가능한 결과가 있는 확률 변수 X가 있을 때, 이러한 시험을 1 회 시행하고 이때 가능한 확률 변수 X의 분포
  - 카테고리 확률변수(Categorical random variable)는 1부터 $K$ 까지 $K$ 개 정숫값 중 하나가 나온다. 이 정숫값을 범주값, 카테고리(category) 혹은 클래스(class)라고 한다. (주사위 던지기)
  - $k$ 개의 카테고리 중 하나가 나타날 확률을 의미한다.
- 다항 분포
  - 카테고리 분포의 시행의 확률변수가 여러개 존재하며 n 번 시행할 때 각각의 확률 변수들이 나타내는 값의 특정 횟수에 대한 분포
  - 여러 개의 독립 확률변수들에 대한 확률분포로써 여러 번의 독립시행에서 각각의 값이 특정 횟수가 나타날 확률분포로써 이항분포에서 확장된 분포로 생각 할 수 있음 (베르누이 분포 -> 카테고리 분포)
- 가우시안 정규 분포
  - 자연 현상에서 나타나는 숫자를 확률 모형으로 나타낼 때 사용한다. bell shape을 가지고 있다.
  - 정규분포는 평균과 표준편차가 주어져 있을 때 엔트로피를 최대화 하는 분포이다.
  - 정규분포곡선은 좌우 대칭이며 하나의 꼭지를 가진다.
- t 분포
  - https://m.blog.naver.com/sendmethere/221333164258
  - 독립된 두 집단 (또는 대응표본t검정의 경우에는 한 집단)의 평균 차이가 있는지를 검사하는 방법이다
  - 모집단의 분산이나 표준편차를 알지 못할 때 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법으로 “두 모집단의 평균간의 차이는 없다”라는 귀무가설과 “두 모집단의 평균 간에 차이가 있다”라는 대립가설 중에 하나를 선택할 수 있도록 하는 통계적 검정방법
  - 평균 검정을 하기 위해 고안되었다는 점
    - 모집단이 정규분포를 따른다고 하면, 표본평균은 N(μ,σ2n) 을 따른다는 것을 기억하실 겁니다. 그래서 과거에는 이를 이용하여 평균 검정을 해왔는데, 일반적으로 우리는 모분산인 σ2 을 알 길이 없습니다
    - 표본 수가 작을 때는 정확한 모분포의 std 를 모르는 것이 큰 문제가 될 수 있습니다.
    - 모분산 σ2 을 정확히 알 수 없을 뿐 아니라, 그 값에 따라 정규분포의 모양이 크게 좌지우지되어, 정규분포를 이용한 검정이 그 신뢰성을 잃게되기 때문.
    - 정규분포와 형태는 비슷하지만 모분산 항을 포함하고 있지 않고, 대신 표본분산을 이용한 분포를 고안해 내는데, 그것이 t분포
      - 즉, 모분산의 std를 알수 없으니, 모분산의 std를 사용하지 않고 표본의 std를 이용하여 표본의 분포를 만들어 낸 것
  - t 분포는 정규분포의 평균의 해석에 많이 활용되는 분포
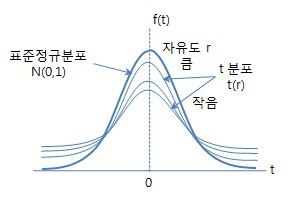
  - 0을 중심으로 대칭 (중심은 0으로 고정) 이고 종모양을 하고 있습니다. 표준정규분포와 상당히 유사한 모습을 가지나, 양 꼬리부분에 상대적으로 많은 확률이 존재하여 두꺼운 꼬리를 갖는 것이 차이점입니다.
  - 표준정규분포와 중심이 같고 자유도(degree of freedom, df)에 따라 종의 형태가 조금씩 변화합니다. df는 표본 수와 관련이 있는 개념으로, 표본이 많아지면 표준정규분포와 거의 동일한 형태를 보입니다.
    - 이는 표본 수가 적은데서 나오는 우연에 의한 극단적인 값에 대해서도 어느정도 유연한 검정 결과를 준다고 할 수 있습니다.
- 카이제곱 분포
  - 이제곱분포에서 카이( $χ$ )는 $X$ 의 그리스 알파벳 버전으로 평균 0, 분산 1인 표준정규분포를 의미한다. 따라서 카이제곱이라는 이름에는 표준정규분포를 제곱한다는 의미가 내포
  - 자유도 $v$ 인 카이제곱분포는 $X^{2}$ 을 $v$ 개 합한 것의 분포
- F 분포
  - 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산비율을 나타내는 연속 확률 분포입니다. F-분포의 쓰임새는 두 가지 이상의 표본집단의 분산을 비교하거나 모집단의 분산을 추정할 때 쓰입니다.
  - 2개 이상의 표본평균들이 동일한 모평균을 가진 집단에서 추출되었는지 아니면 서로 다른 모집단에서 추출된 것인지를 판단하기 위하여 이용하는 것이 F-분포입니다.
- 감마 분포
  - 감마 분포는 $α$ 개의 사건이 일어날 때까지 걸리는 대기 시간에 대한 분포
  - 지수 분포는 사건이 1번 일어날 때까지 걸리는 시간에 대한 것이었습니다. 바로 감마 분포는 지수 분포를 한 번의 사건이 아닌 여러 개의 사건으로 확장한 것
  - 모수의 베이지안 추정에 사용된다. 다만 베타분포가 0부터 1 사잇값을 가지는 모수를 베이지안 방법으로 추정하는 데 사용되는 것과 달리 감마분포는 0부터 무한대의 값을 가지는 양수 값을 추정하는 데 사용
- 베타 분포
  - 베타분포는 0과 1사이의 값을 가지는 단일(univariate) 확률변수의 베이지안 모형에 사용
  - 베타분포는 0부터 1까지의 값을 가질 수 있는 베르누이분포의 모수 p의 값을 베이지안 추정한 결과를 표현한 것이다.
    - 베이지안 추정이란?
      - 모수가 가질 수 있는 모든 값에 대해 가능성을 확률분포
- 디리클레 분포
  - 디리클레분포는 0과 1사이의 사이의 값을 가지는 다변수(multivariate) 확률변수의 베이지안 모형에 사용
  - 디리클레분포란 $k$ 차원의 실수 벡터 중 벡터의 요소가 양수이며 모든 요소를 더한 값이 1인 경우에 확률값이 정의되는 연속확률분포
  - 베타 분포 <- 이항 분포 (베르누이 분포) 이므로 디리클레 분포 <- 다항 분포 (카테고리 분포)

[통계교육] 풀어쓰는 통계 - t 검정(t-test)이란?

1. t 검정을 비롯한 관련 용어 설명 2. t 검정의 특징 t검정의 특징을 정리하자면 다음과 같다. 3. t 검정...

blog.naver.com

[통계교육] 풀어쓰는 통계 - t 검정(t-test)이란?

1. t 검정을 비롯한 관련 용어 설명 2. t 검정의 특징 t검정의 특징을 정리하자면 다음과 같다. 3. t 검정...

blog.naver.com

조건부 확률은 무엇일까요?
- 한 사건이 일어난다는 것을 전제로 할 때 다른 사건이 일어날 확률을 조건부 확률이라고함.
공분산과 상관계수는 무엇일까요? 수식과 함께 표현해주세요
- 공분산
  - 두 확률변수 X와 Y가 어떤 모양으로 퍼져있는지
  - 즉, X가 커지면 Y도 커지거나 혹은 작아지거나 아니면 별 상관 없거나 등을 나타내어 주는 것이다.
- 상관계수
  - 공분산의 특징상 확률변수 X와 Y의 값의 range가 크다면 작은 경우에 비해서 상대적으로 큰 값이 발생하지만 실제로는 작은 range에서의 COV보다 상관 관계가 적을 수 있다. 즉 normalization을 수행하여 comparison이 가능하도록 하는 방법이 상관계수
  - 상관계수의 절대값은 1을 넘을 수 없다.2. 확률변수 X, Y가 독립이라면 상관계수는 0이다.3. X와 Y가 선형적 관계라면 상관계수는 1 혹은 -1이다.
  - 양의 선형관계면 1, 음의 선형관계면 -1
신뢰 구간의 정의는 무엇인가요?
- 표본 데이터를 사용하여 모집단 모수 (ex., 정규분포라면 평균과 std) 를 추정하고자 하는 경우 당연한 말이지만 불확실성은 sampling에서 기인합니다.
- 구간추정시 표본의 평균값(Point)이 해당 모 분포의 평균에서 1 std 내에 포함되있을 가능성..이 95%, 97.5% 등등을 의미합니다. 즉, 표본으로부터 모집단을 얼마나 신뢰성있게 추론할 수 있는지를 의미합니다.
  - p-value 계산의 특징 중 하나는 효과의 크기(effect size)이고 또 다른 하나는 표본의 크기(n수)이다. 그런데, p-value는 이 두 정보들을 숫자 하나에 표현하였다. 그래서 만약 우리의 실험 결과로써 매우 작은 p-value를 얻었다고 해보자. 그렇다고 한들 귀무가설을 기각할 수 있다는 사실의 원인이 과연 효과의 크기가 충분히 커서인지, 아니면 표본의 크기가 크다 보니 얻게 된 결과인지는 p-value 값 만으로는 충분히 알 수가 없다는 것이다
p-value를 고객에게는 뭐라고 설명하는게 이해하기 편할까요?
- 가설이 맞는다는 가정 하에, 내가 현재 구한 통계값이 얼마나 자주 나올 것인가를 의미
  - p-value는 가설검정이라는 것이 sampling 된 데이터를 갖고 하는 것이기 때문
  - 가설검증이라는 것은 전체 데이터의 일부만을 추출하여 평균을 내고, 그 평균이 전체 데이터의 평균을 잘 반영한다는 가정 하에 전체 데이터의 평균을 구하는 작업인데, 아무리 무작위 추출을 잘 한다 하더라도 추출된 데이터의 평균은 전체 데이터의 평균에서 멀어질 수 있게 된다.
    - 진짜 random 의 경우 1억번 로또가 다 실패할수도있지 않는가 ... 즉 정규분포의 꼬리에서만 랜덤하게 추출될수도있다는 걸 생각하는것이지 ...
  - 따라서, 내가 추출한 이 데이터의 평균이 원래의 전체 데이터의 평균과 얼마나 다른 값인지를 알 수 있는 방법이 필요하게 된다. 이와 같은 문제 때문에 나온 값이 p-value 이다.
p-value는 요즘 시대에도 여전히 유효할까요? 언제 p-value가 실제를 호도하는 경향이 있을까요?
- 실제로 표본의 크기가 2억 정도되면 p-value는 작아질 수 밖에 없다. 즉, 데이터가 많으면 작은 차이라도 발견해 낼 수 있어 가설검정의 틀린점을 찾아낼 수 있게 되고 현대 사회에서 빅데이터를 다루는 경우에 이러한 현상이 쉽게 일어날 수 있다.
A/B Test 등 현상 분석 및 실험 설계 상 통계적으로 유의미함의 여부를 결정하기 위한 방법에는 어떤 것이 있을까요?
- AB Test란 디지털 환경에서 전체 실사용자를 대상으로 대조군(Control Group)과 실험군(Experimental Group)으로 나누어서 어떤 특정한 UI나 알고리즘의 효과를 비교하는 방법론입니다.
- 단순히 트래픽 비율을 나누는 방법만을 알고 있습니다. 하지만 실제 AB Test를 수행할 때 서로 다른 대조군과 실험군을 보여주는 방법에는 (1)노출빈도분산 방식과 (2)사용자분산 방식, (3)시간대분산 방식의 3가지 방식이 존재합니다.
R square의 의미는 무엇인가요?
- 1-(추정 모형의 MSE / 평균 관측 값의 MSE)
  - 분모 : observed 들의 평균 - 새 관찰 값
  - 분자 : 추정 값 - 새 관찰 값
- 모델의 추정능력이 떨어질수록 값이 감소
- R-square가 1에 가깝다는 의미는 회귀선이 데이터에 fit
- 설계한 모형의 오차가 작다면 R-square가 커지게 될 것이고, 설계한 모형의 오차가 크다면 R-square가 작아지게 되는 것이다.
평균(mean)과 중앙값(median)중에 어떤 케이스에서 뭐를 써야할까요?
- 데이터의 분포가 정규분포에 가까울때는 mean과 median이 비슷하거나 같겠지만, 좌우로 비대칭일경우 mean이 median보다 크거나 작을 수 있음 이럴경우 분석에 median을 사용함이 유용함
- 데이터가 충분치 않은 경우 ML에서 샘플들의 mean 값을 추론하게 학습이 될 가능성이 높음. 이 경우 시계열 예측에서는 historical average와 같은 단순한 형태가 되는게 빈번함.
중심극한정리는 왜 유용한걸까요?
- t 검정이나 F 분포를 통한 검정을 사용할 때 데이터의 수가 큰 경우 중심극한정리를 따라 normal distribution으로 가정하고 검정을 수행할 수 있기 때문에.
엔트로피(entropy)에 대해 설명해주세요. 가능하면 Information Gain도요.
- 놀라게 하는 정도
- 새로운 feature 가 추가되었을 때 얼마나 많은 Entorpy를 줄여주는가 ... 정보량의 제공량
요즘같은 빅데이터(?)시대에는 정규성 테스트가 의미 없다는 주장이 있습니다. 맞을까요?
- n이 크다 ! p-value가 작아질수밖에 ...
어떨 때 모수적 방법론을 쓸 수 있고, 어떨 때 비모수적 방법론을 쓸 수 있나요?
- 정규성을 갖는다는 모수적 특성을 이용하는 통계적 방법 군당 30명 이상으로 구성된 표본의 경우 정규분포를 따른다고 가정한다.
  - * 중심극한정리 : 본래의 분포에 상관없이 무작위로 복원추출된 연속형 자료의 평균의 분포는 정규분포를 따른다.
- cluster 당 10개 이하의 sample들로 구성된 cluster에 대한 통계적 수치를 검증하고자 할 때 sampling으로 얻게 된 자료의 평균의 분포가 정규분포를 따른다고 가정할 수 없어 비모수적 방법을 써야함.
  - 1) 정규성 검정에서 정규분포를 따르지 않는다고 증명되거나
  - 2) 표본의 수가 적어 정규분포를 가정할 수 없는 경우
  - 3) 모집단에 대한 아무런 정보가 없는 경우
“likelihood”와 “probability”의 차이는 무엇일까요?
- Probability = 우리가 아는 확률 (확률변수 X가 발생할 확률) (확률 분포는 고정)
- Likelihood는 확률분포함수(PDF)의 y 값 (확률변수 X가 일어낫을때 어떤 분포의 모수에서 얼마나 일어날 수 있는지 확률)
통계에서 사용되는 bootstrap의 의미는 무엇인가요.
- 가상의 샘플링횟수. 조사된 결과를 바탕으로 정확성을 평가하거나 분포를 추정하는것 (Random Forest 등에서 볼 수 있음)
모수가 매우 적은 (수십개 이하) 케이스의 경우 어떤 방식으로 예측 모델을 수립할 수 있을까요?
베이지안과 프리퀀티스트간의 입장차이를 설명해주실 수 있나요?
검정력(statistical power)은 무엇일까요?
missing value가 있을 경우 채워야 할까요? 그 이유는 무엇인가요?
아웃라이어의 판단하는 기준은 무엇인가요?
콜센터 통화 지속 시간에 대한 데이터가 존재합니다. 이 데이터를 코드화하고 분석하는 방법에 대한 계획을 세워주세요. 이 기간의 분포가 어떻게 보일지에 대한 시나리오를 설명해주세요
출장을 위해 비행기를 타려고 합니다. 당신은 우산을 가져가야 하는지 알고 싶어 출장지에 사는 친구 3명에게 무작위로 전화를 하고 비가 오는 경우를 독립적으로 질문해주세요. 각 친구는 2/3로 진실을 말하고 1/3으로 거짓을 말합니다. 3명의 친구가 모두 “그렇습니다. 비가 내리고 있습니다”라고 말했습니다. 실제로 비가 내릴 확률은 얼마입니까?
필요한 표본의 크기를 어떻게 계산합니까?
Bias를 통제하는 방법은 무엇입니까?
로그 함수는 어떤 경우 유용합니까? 사례를 들어 설명해주세요
- 정규성을 높이고 분석(회귀분석 등)에서 정확한 값을 얻기 위함이다.
- 데이터 간 편차를 줄여 왜도1(skewness)와 첨도2(Kurtosis)를 줄일 수 있기 때문에 정규성이 높아진다.
  - 예를 들어, 연령 같은 경우에는 숫자의 범위가 약 0세~120세 이하 이겠지만, 재산 보유액 같은 경우에는 0원에서 몇 조단위까지 올라갈 수 있다. 즉, 데이터 간 단위가 달라지면 결과값이 이상해 질 수 있다.
- log의 역할은 큰 수를 같은 비율의 작은 수로 바꿔 주는 것이다.
- 즉, 데이터 간의 편차가 큰 경우에 로그를 취하면 의미있는 결과를 얻을 가능성이 높아진다.
- 분포가왼쪽으로 치우쳐져있을때 로그를취하면 대략적인 정규분포가 이루어지며, NLP에서 TF-IDF계산시 log를 취하는데 이는 스케일을 작게만들기위함임

[https://yongwookha.github.io/MachineLearning/2021-01-29-interview-question]

분석 일반

좋은 feature란 무엇인가요. 이 feature의 성능을 판단하기 위한 방법에는 어떤 것이 있나요?
“상관관계는 인과관계를 의미하지 않는다”라는 말이 있습니다. 설명해주실 수 있나요?
A/B 테스트의 장점과 단점, 그리고 단점의 경우 이를 해결하기 위한 방안에는 어떤 것이 있나요?
각 고객의 웹 행동에 대하여 실시간으로 상호작용이 가능하다고 할 때에, 이에 적용 가능한 고객 행동 및 모델에 관한 이론을 알아봅시다.
고객이 원하는 예측모형을 두가지 종류로 만들었다. 하나는 예측력이 뛰어나지만 왜 그렇게 예측했는지를 설명하기 어려운 random forest 모형이고, 또다른 하나는 예측력은 다소 떨어지나 명확하게 왜 그런지를 설명할 수 있는 sequential bayesian 모형입니다.고객에게 어떤 모형을 추천하겠습니까?
고객이 내일 어떤 상품을 구매할지 예측하는 모형을 만들어야 한다면 어떤 기법(예: SVM, Random Forest, logistic regression 등)을 사용할 것인지 정하고 이를 통계와 기계학습 지식이 전무한 실무자에게 설명해봅시다.
나만의 feature selection 방식을 설명해봅시다.
데이터 간의 유사도를 계산할 때, feature의 수가 많다면(예: 100개 이상), 이러한 high-dimensional clustering을 어떻게 풀어야할까요?

머신러닝

Cross Validation은 무엇이고 어떻게 해야하나요?
- CV는 train set에서의 데이터 일부씩 모든 데이터를 사용하여 validation을 하고 모델의 성능을 평균으로 측정하는 것
- 특정 구간에서만 잘하는 모델에 대한 방지를 가능케 한다
회귀 / 분류시 알맞은 metric은 무엇일까요?
- MSE
- Cross-Entroy
알고 있는 metric에 대해 설명해주세요(ex. RMSE, MAE, recall, precision …)
정규화를 왜 해야할까요? 정규화의 방법은 무엇이 있나요?
Local Minima와 Global Minima에 대해 설명해주세요.
차원의 저주에 대해 설명해주세요
dimension reduction기법으로 보통 어떤 것들이 있나요?
PCA는 차원 축소 기법이면서, 데이터 압축 기법이기도 하고, 노이즈 제거기법이기도 합니다. 왜 그런지 설명해주실 수 있나요?
- PCA는 분산이 최대가 되도록 하는 축을 찾고, 그 축과 직교하면서 분산이 최대가 되도록 하는 축을 이어 찾아나가는 방식으로 데이터를 간단히 표현합니다.
LSA, LDA, SVD 등의 약자들이 어떤 뜻이고 서로 어떤 관계를 가지는지 설명할 수 있나요?
- LSA(Latent Semantic Analysis, 잠재의미분석) : SVD를 이용하여 차원을 축소
  LDA(Latent Dirichlet Allocation, 잠재디리클레할당) : 주제별 단어분포와 문서별 주제 분포를 학습하여 Topic Modeling 하는 방법
  SVD(Singular Value Decomposition) : 특이값 분해
Markov Chain을 고등학생에게 설명하려면 어떤 방식이 제일 좋을까요?
- 어제의 날씨가 오늘의 날씨에 영향을 미치는 방식 (비가 왓으니 오늘은 춥다)
- 반대로 MDP 가 아니면, 방금 주사위가 5가 나왓다고 이제 6이 나오는건 관계가 없는 문제.
텍스트 더미에서 주제를 추출해야 합니다. 어떤 방식으로 접근해 나가시겠나요?
SVM은 왜 반대로 차원을 확장시키는 방식으로 동작할까요? 거기서 어떤 장점이 발생했나요?
- SVM을 비선형 분류 모델로 사용하기 위해 저차원 공간의 데이터를 고차원 공간으로 매핑하여 선형 분리가 가능한 데이터로 변환하여 처리한다.
- 즉, 선형 분리를 할 수 있도록 하는 feature space로 매핑 하는 것
다른 좋은 머신 러닝 대비, 오래된 기법인 나이브 베이즈(naive bayes)의 장점을 옹호해보세요.
- 1. 결과 도출을 위해 조건부 확률만 계산하면 되므로 매우 빠르고, 메모리를 많이 차지하지 않는다.
  2. 데이터가의 특징들이 서로 독립되어 있을 때 좋은 결과를 얻을 수 있다.
  3. 데이터의 양이 적더라도 학습이 용이하다.
Association Rule의 Support, Confidence, Lift에 대해 설명해주세요.
- Support : X와 Y 두 item이 얼마나 자주 발생하는지를 의미
- Confidence : X가 발생했을 떄, Y도 포함되어 있는 비율
- Lift : X가 발생하지 않았을 때의 Y 발생 비율과 X가 발생했을 때 Y 발생 비율의 대비. 숫자가 1보다 크거나 작은 정도에 따라 연관성을 파악할 수 있다.
최적화 기법중 Newton’s Method와 Gradient Descent 방법에 대해 알고 있나요?
- Newton’s Method는 연속적이고 미분 가능한 함수에 대해 무작위 값을 대입해서 결과값의 변화 추이를 통해 원하는 해를 근사하는 방법이다.
- Gradient Descent 방법은 함수의 극대, 극소를 찾는 방법이며, 마찬가지로 지점에서의 미분값에 따라 대입할 값을 갱신하므로 그 근본적인 방법은 동일하다.
머신러닝(machine)적 접근방법과 통계(statistics)적 접근방법의 둘간에 차이에 대한 견해가 있나요?
- 전자의 경우 머신이 스스로 학습하여 결정하며, 후자의 경우엔 사람이 직접 해결 방법을 설정한다.
인공신경망(deep learning이전의 전통적인)이 가지는 일반적인 문제점은 무엇일까요?
지금 나오고 있는 deep learning 계열의 혁신의 근간은 무엇이라고 생각하시나요?
ROC 커브에 대해 설명해주실 수 있으신가요?
- True Positive(TP) : 실제 True인 정답을 True라고 예측 (정답)
- False Positive(FP) : 실제 False인 정답을 True라고 예측 (오답)
- False Negative(FN) : 실제 True인 정답을 False라고 예측 (오답)
- True Negative(TN) : 실제 False인 정답을 False라고 예측 (정답)
- <예측이 맞 or 틀> <예측> : <예측>이라고 했는데 그 예측이 <맞 or 틀>
여러분이 서버를 100대 가지고 있습니다. 이때 인공신경망보다 Random Forest를 써야하는 이유는 뭘까요?
- 일반적으로 각 단계별로 의존적인 end-to-end 인공신경망과 달리 Random Forest는 여러개의 독립적인 decision tree를 이용하여 결과를 투표하는 형식이므로 다수의 서버에서 병렬적인 처리가 용이하다.
K-means의 대표적 의미론적 단점은 무엇인가요? (계산량 많다는것 말고)
- K개의 Cluster를 미리 입력받아 Expectation과 Maximization 단계를 거듭하여 군집화를 수행한다. 단점들은 다음과 같다.
  1. 초기에 사용자가 해당 데이터에 몇개의 Cluster가 있는지 알고 있어야 한다.
  2. K개의 Cluster를 초기화하는 방법에 따라 결과에 큰 차이가 있다.
  3. 클러스터의 모양이 구형이 아닌 경우, 적용이 힘들다.
  4. Maximization단계에서 각 데이터들과의 거리를 기준으로 Cluster 중심점의 위치를 업데이트하므로 데이터의 노이즈에 민감하게 반응한다.
L1, L2 정규화에 대해 설명해주세요
- 너무 큰 파라메터의 영향력을 줄이는 전략이다.
XGBoost을 아시나요? 왜 이 모델이 캐글에서 유명할까요?
앙상블 방법엔 어떤 것들이 있나요?
- 앙상블 방법에는 서로 다른 모델들을 학습시켜 결과를 투표하는 Voting
- 같은 모델을 다른 Train data로 학습시키는 Bagging(Bootstrap aggregating) & Pasting
- 여러개의 약한 분류기를 결합하여 높은 성능의 모델을 도출하는 Boosting (ex) XGBoost 는 weak classifier가 낸 output과 정답의 오차를 target으로하는 weak classifier를 연속으로 붙이는 방법 (gradient라는 이름은 이 loss 가 gradient형태이기 때문)
SVM은 왜 좋을까요?
- SVM은 데이터들을 선형 분리하며 최대 마진의 초평면을 찾는 크게 복잡하지 않은 구조이며, 커널 트릭을 이용해 차원을 늘리면서 비선형 데이터들에도 좋은 결과를 얻을 수 있다.
- 또한 이진 분류 뿐만 아니라 수치 예측에도 사용될 수 있다.
- Overfitting 경향이 낮으며 노이즈 데이터에도 크게 영향을 받지 않는다. (margin hyperparameter 조절 가능!)
feature vector란 무엇일까요?
- Data의 Feature들을 담고있는 vector
좋은 모델의 정의는 무엇일까요?
- Generalization이 잘 된 모델
50개의 작은 의사결정 나무는 큰 의사결정 나무보다 괜찮을까요? 왜 그렇게 생각하나요?
- 다른 weight 가 학습되어 ensemble voting등의 방법으로 overfitting을 방지할 수 있다
- 학습에서 Multi-GPU 학습등에 용이하다
스팸 필터에 로지스틱 리그레션을 많이 사용하는 이유는 무엇일까요?
- linear regression의 output에 sigmoid를 사용하여 binary classification을 수행
- 단순하며 적은 데이터에도 효과적 MLE (P(weight | data) 를 학습)
OLS(ordinary least squre) regression의 공식은 무엇인가요?
- MSE loss function사용하는 Linear Regression

딥러닝 일반

딥러닝은 무엇인가요? 딥러닝과 머신러닝의 차이는?
- 딥러닝은 인공신경망을 깊은 구조로 설계하여 비선형성이 높은 문제들을 해결하는 방법을 통칭한다.
  - activation function을 사용
왜 갑자기 딥러닝이 부흥했을까요?
- hardware의 발전. 수많은 연산이 가능해짐.
마지막으로 읽은 논문은 무엇인가요? 설명해주세요
- Normalizing Flow 와 서울대 팀의 Transformer 기반 Time Seires 예측 논문 in 주식 벤치마크
Cost Function과 Activation Function은 무엇인가요?
- cost function은 ML 모델을 학습시키기위해 추정값과 true 값의 차이를 계산하는 함수
- activation function은 ML layer를 딥 하게쌓기 위해 layer 간 non-linearity를 부여하여 각 layer 를 지날 때 마다 feature space를 변환해 문제를 해결할 수 있는 space로 만들 수 있게 해주는 함수?
Tensorflow, Keras, PyTorch, Caffe, Mxnet 중 선호하는 프레임워크와 그 이유는 무엇인가요?
- Pytorch가 최근에 회사에서 사용해서 익숙. 일반적으로 편함 그러나 TF2.0되면서 비슷할 듯
- TF가 Tensorflow TFX가 있어서 deploy에 매우 유리하며 JAX도 통합이 쉬워 더 좋을 것도 같으나 현재 사용해보지는 못했음.
Data Normalization은 무엇이고 왜 필요한가요?
알고있는 Activation Function에 대해 알려주세요. (Sigmoid, ReLU, LeakyReLU, Tanh 등)
- Sigmoid
- ReLU
  - 기울기가 0에서 1사이 값이 아닌 '1'이기 때문에 Gradient Vanishing 문제를 해결하였다
  - x가 음수면 그 결과로 전부 0을 출력하기 때문에 몇몇 가중치들이 갱신되지 않는 문제가 발생
- LeakyReLU
- Tanh
오버피팅일 경우 어떻게 대처해야 할까요?
하이퍼 파라미터는 무엇인가요?
Weight Initialization 방법에 대해 말해주세요. 그리고 무엇을 많이 사용하나요?
볼츠만 머신은 무엇인가요?
요즘 Sigmoid 보다 ReLU를 많이 쓰는데 그 이유는?
- Non-Linearity라는 말의 의미와 그 필요성은?
  - 선현 결합 (기본 사칙연산의 조합)으로써 값을 표현할 수 없는 경우
  - 선형 함수: 직선 1개로 그릴 수 있는 함수. y = ax+b의 형태.
  - 비선형 함수: 직선 1개로 그릴 수 없는 함수. sigmoid나 ReLU 같은 함수.
- ReLU로 어떻게 곡선 함수를 근사하나?
  - ReLU는 선형 부분과 비선형 부분이 결합된 모양이다. ReLU가 반복 적용되면서 선형 부분의 결합이 이루어지고, 곡선 함수를 근사할 수 있게 된다.
- ReLU의 문제점은?
  - ReLU는 0이하의 입력을 모두 0으로 내보낸다. 이 과정에서 정보의 손실이 불가피하다. 이런 단점을 보완하기 위해 Leaky ReLU와 같이 0이하 값도 출력에 반영하는 활성화 함수들이 등장했다.
- Bias는 왜 있는걸까?
  - Bias는 함수의 모양을 변경하지 않고 Shift해주어 정답에 근사할 수 있도록 도와준다.
Gradient Descent에 대해서 쉽게 설명한다면?
- 왜 꼭 Gradient를 써야 할까? 그 그래프에서 가로축과 세로축 각각은 무엇인가? 실제 상황에서는 그 그래프가 어떻게 그려질까?
- GD 중에 때때로 Loss가 증가하는 이유는?
- 중학생이 이해할 수 있게 더 쉽게 설명 한다면?
- Back Propagation에 대해서 쉽게 설명 한다면?
Local Minima 문제에도 불구하고 딥러닝이 잘 되는 이유는?
- GD가 Local Minima 문제를 피하는 방법은?
  - Momentum 등의 개념을 도입한 RMSprop, Adam 등의 Optimization 전략을 사용한다.
- 찾은 해가 Global Minimum인지 아닌지 알 수 있는 방법은?
  - Global Minima가 정확히 어디에 존재하는지는 알 수 없다. 다만, 학습에 사용하지 않은 Test Dataset에 대한 성능을 평가하는 것으로 모델이 Global Minima에 가까운지 유추할 수 있다.
Training 세트와 Test 세트를 분리하는 이유는?
- Validation 세트가 따로 있는 이유는?
  - 모델 학습 과정 중, Training data와 분리된 Validation data로 모델을 평가하여 그 결과를 학습에 반영하므로써 Training Data에 대한 Overfitting을 방지하는 효과가 있다.
- Test 세트가 오염되었다는 말의 뜻은?
  - Test data에 Training data와 일치하거나, 매우 유사한 데이터들이 포함되어 Test data가 General한 상황에서의 성능 평가를 수행하지 못함을 말한다.
- Regularization이란 무엇인가?
  - 단순히 Cost function의 값이 작아지는 방향으로 모델을 학습하면 특정 가중치가 과도하게 커지는 현상이 나타날 수 있다. Regularization의 개념은, Cost Function을 계산할 때 가중치의 절대값 만큼을 더해주는 방법으로 특정 가중치의 값이 너무 커지는 현상을 억제하는 것이다.
Batch Normalization의 효과는?
- 은닉층에서의 입력값을 Normalize함으로써 입력 분포를 조정 할 수 있다.
- GD 과정에서 Variance를 낮춰 학습이 효율적으로 이뤄질 수 있다.
- Local Optima를 피할 가능성이 높아진다.
Dropout의 효과는?
BN 적용해서 학습 이후 실제 사용시에 주의할 점은? 코드로는?
GAN에서 Generator 쪽에도 BN을 적용해도 될까?
- 그 이유는 Discriminator가 조작되지 않은 Generator의 결과물의 정확한 값으로 mean, scale을 학습하기 위함이다.
SGD, RMSprop, Adam에 대해서 아는대로 설명한다면?
- SGD에서 Stochastic의 의미는?
  - Stochastic Gradient Descent는 Train Dataset을 전부 이용하는 Batch Gradient Descent와 달리, mini-batch를 이용하여 loss function을 이용한다.
  - ‘Stochastic’은 mini-batch가 전체 train dataset에서 무작위로 선택된다는 것을 의미한다. (train set 에서 sampling을 통해 구성한 mini-batch를 통해서 학습을 한다는 것을 의미)
간단한 MNIST 분류기를 MLP+CPU 버전으로 numpy로 만든다면 몇줄일까?
- 어느 정도 돌아가는 녀석을 작성하기까지 몇시간 정도 걸릴까?
- Back Propagation은 몇줄인가?
- CNN으로 바꾼다면 얼마나 추가될까?
간단한 MNIST 분류기를 TF, Keras, PyTorch 등으로 작성하는데 몇시간이 필요한가?
- CNN이 아닌 MLP로 해도 잘 될까?
  - 이전엔 모르겠었으나, MLP mixer를 생각해보면 모델 구조에 따라서 잘 될 수 있을 것이라 생각됨.
- 마지막 레이어 부분에 대해서 설명 한다면?
  - softmax layer 가 달려있어야 model의 output이 logits 가 될 수 있기 떄문에 softmax layer가 될 것.
  - 마지막 layer가 cnn인것을 물어본 것이라면 high-level feature인 복잡한 모양 (8 과 5의 차이를 구별)하는 layer가 학습 될 것
- 학습은 BCE loss로 하되 상황을 MSE loss로 보고 싶다면?
  - - https://simpling.tistory.com/entry/Mean-Squared-Error-VS-Cross-Entropy-Error
  - Cross Entropy에서 Entropy는 물리학을 배울 때 자주 나오는 단어인데 불확실성의 정도
  - A후보가 이기는 경우: -log(P(A)) = -log(0.9) = 0.05
  - B후보가 이기는 경우: -log(P(B)) = -log(0.1) = 1.0이다.

- - Entropy는 놀람의 정보의 평균이므로 0.9*0.05+ 0.1*1.0 = 0.15이다.
  - 이번에는 A후보와 B후보의 지지율이 50:50이라고 생각해보겠다. 이때 각 후보의 Entropy는 0.30이다. 이때의 Entropy는 0.5*0.3 + 0.5*0.3 = 0.3이다.
  - 즉, 정답에 대한 추정 y_hat에 높은 확률을 주고 정답이 아닌 경우들에 대해서 낮은 확률 y_hat을 추론해 내도록 모델을 학습하는 것.
  - MSE의 경우 $▽_{a} C ⊙ σ^{'} (Z^{L})$ 로 구하는데 CEE는 σ′(ZL)σ′(ZL)항을 사용하지 않아 역전파시 기울기 손실이 덜하며 속도도 더 빠르다. 그러므로 CEE는 역전파에 유리한 함수

작은 minibatch 사용의 문제점 과 장점?
- Mini-batch의 사이즈가 작으면 한 iteration의 계산량이 적어지기 때문에 step당 속도가 빨라지며 적은 Graphic Ram으로도 학습이 가능하는 장점이 있다.
- 하지만 Target의 Variance가 큰 경우 (true target의 variance가 큰 경우) sample 된 데이터 batch별로 variance가 커져 학습에 어려움이 생길 수 있다
  - mini-batch-size가 너무 작을 때는 학습데이터에 대한 대표성이 떨어져 학습의 일반성(Generalization)이 불리할 수 있다.
Momentum loss 의 수식
- $w (t) = m \cdot w (t - 1) - α \frac{\partial}{\partial w} Cost (w)$
  $m$ 은 모멘텀 상수 (default=0.9)
- w_{t_1} 의 영향을 고려하는것이 momentum 이므로
딥러닝할 때 GPU를 쓰면 좋은 이유는?
- GPU에는 부동소수점 계산에 특화된 수많은 코어가 있어, Matrix Multiplication이 핵심인 Deep Learning에서 병렬 처리를 수행 하기에 유리하다.
학습 중인데 GPU를 100% 사용하지 않고 있다. 이유는?

Batch Size가 작다.
모델의 Size가 작다.
CPU의 overhead가 병목이 되어 GPU에서 일어나는 모델과 관련된 연산 (inference, backward) 등이 자주 일어나지 못한다.

GPU를 두개 다 쓰고 싶다. 방법은?
- pytorch의 경우 dataparallel이 있으나 GPU를 고르게 사용하지 못함.
- DistributedDataParallel 기법을 사용하면 고르게 사용할 수 있으며, k8s와 적용할 경우 다른 node에 있는 gpu도 사용할 수 있음.
학습시 필요한 GPU 메모리는 어떻게 계산하는가?
- 데이터 메모리 + 모델의 메모리 + backward시 gradient의 메모리 까지 고려
- Trainable Parameter의 개수에 4byte(FP16) 또는 8byte(FP32)를 곱하면 DL 모델의 GPU 메모리 사용량을 대략적으로 알 수 있다. 그리고 여기에 input data의 tensor size를 더하면 된다.
- Optimizer의 variable, model forward 과정에서 쓰이는 temporary variable 등이 있다.
TF, Keras, PyTorch 등을 사용할 때 디버깅 노하우는?
- PyTorch의 경우 stop point 활용이 가능하기 때문에 random seed를 고정 (cuda, numpy, python 등 모두 고정, set deterministic) 한 후 입력값과 weight를 계산이 가능한 값 (예 1로 init) 하여 변화를 감시
뉴럴넷의 가장 큰 단점은 무엇인가? 이를 위해 나온 One-Shot Learning은 무엇인가?
- validation을 잘하는 것이 test results 에서 좋은 성능을 보인다는 것을 보장하지 못한다.
- 실제로 data drift (concept drift) 에 매우 취약하며, One-Shot Learning은 test 를 위한 케이스를 1번씩만 보여주고 학습하는 방법으로 경험을 하게하는 것.
- 뉴럴넷을 학습시킨다면 굉장한 overfit이 일어날 수 밖에 없다. 파라미터는 많고 데이터는 매우 적기 때문

강화학습

MDP는 무엇일까요?
가치함수는 무엇일까요? 수식으로도 표현해주세요
벨만 방정식은 무엇일까요? 수식으로도 표현해주세요
강화학습에서 다이나믹 프로그래밍은 어떤 의미를 가질까요? 한계점은 무엇이 있을까요?
몬테카를로 근사는 무엇일까요? 가치함수를 추정할 때 어떻게 사용할까요?
Value-based Reinforcement Learning과 Policy based Reinforcement Learning는 무엇이고 어떤 관계를 가질까요?
- 만약 value function이 완벽하다면 최적의 policy는 자연스럽게 얻을 수 있습니다. 각 state에서 가장 높은 value를 주는 action만을 선택하면 될 테니까요.
- Policy가 완벽하다면 value function은 굳이 필요하지 않습니다. 결국 value function은 policy를 만들기 위해 사용되는 중간 계산일 뿐이니까요. 이처럼 value function이 없이 policy만을 학습하는 agent를 policy-based라고 부릅니다. Policy Gradient 등이 여기에 해당합니다.
- Value-based RL의 경우는 Q라는 action-value function에 초점을 맞추어서 Q function을 구하고 그것을 토대로 policy를 구하는 방식입니다. Policy-based RL은 Policy자체를 approximate해서 function approximator에서 나오는 것이 value function이 아니고 policy자체가 나옵니다. Policy자체를 parameterize하는 것입니다.Policy Gradient의 장점과 단점은 다음과 같습니다.
  - 기존의 방법의 비해서 수렴이 더 잘되며 가능한 action이 여러개이거나(high-dimension) action자체가 연속적인 경우에 효과적입니다. 즉, 실재의 로봇 control에 적합합니다.
  - 또한 기존의 방법은 반드시 하나의 optimal한 action으로 수렴하는데 policy gradient에서는 stochastic한 policy를 배울 수 있습니다.(예를 들면 가위바위보)
- Value-based RL에서는 Value function을 바탕으로 policy계산하므로 Value function이 약간만 달라져도 Policy자체는 왼쪽으로 가다가 오른쪽으로 간다던지하는 크게 변화합니다. 그러한 현상들이 전체적인 알고리즘의 수렴에 불안정성을 더해줍니다. 하지만 Policy자체가 함수화 되어버리면 학습을 하면서 조금씩 변하는 value function으로 인해서 policy또한 조금씩 변하게 되어서 안정적이고 부드럽게 수렴하게 됩니다.
- value-based RL에서는 Q function을 토대로 하나의 action만 선택하는 optimal policy를 학습하기 때문에 이러한 문제에는 적용시킬수가 없습니다.
- Value-based agent는 데이터를 더 효율적으로 활용할 수 있다는 장점이 있습니다. 이에 비해 policy-based agent는 원하는 것에 직접적으로 최적화를 하기 때문에 더욱 안정적으로 학습된다는 장점이 있습니다.
- 두 극단적인 케이스만 있는 것은 아닙니다. Value function과 Policy를 모두 갖고 있는 agent도 있습니다. 이를 Actor-Critic agent라고 부릅니다.
강화학습이 어려운 이유는 무엇일까요? 그것을 어떤 방식으로 해결할 수 있을까요?
강화학습을 사용해 테트리스에서 고득점을 얻는 프로그램을 만드려고 합니다. 어떻게 만들어야 할까요?
DRL ?
- Policy : Agent의 행동 패턴입니다. 주어진 state에서 어떤 action을 취할지 말해줍니다. 즉, state를 action에 연결 짓는 함수입니다. Policy는 크게 deterministic(결정적) policy와 stochastic(확률적) policy로 나뉩니다. Deterministic policy는 주어진 state에 대해 하나의 action을 주고, stochastic policy는 주어진 state에 대해 action들의 확률 분포를 줍니다.
- Value function : State과 action이 나중에 어느 정도의 reward를 돌려줄지에 대한 예측 함수입니다. 즉, 해당 state과 action을 취했을 때 이후에 받을 모든 reward 들의 가중합입니다. 이때, 뒤에 받을 reward 보다 먼저 받을 reward에 대한 선호를 나타내기 위해 discounting factor $λ$ 를 사용합니다.
DQN
- DQN은 Value-based RL로서 DNN을 이용해 Q-function을 approximate하고 policy는 그것을 통해 만들어졌습니다.
- DQN에서는 TD error를 사용했었습니다
PPO
A2C
DDPG

[강화학습 References]

https://dreamgonfly.github.io/blog/rl-taxonomy/

강화학습 알고리즘 분류 | Dreamgonfly's blog

이 글에서는 강화학습의 여러 알고리즘들을 카테고리로 묶는 분류 체계에 대해서 알아보겠습니다. 분류 체계를 이해하면 새로운 알고리즘이 등장하더라도 기존 알고리즘과 어떤 관계에 있는지

dreamgonfly.github.io

분산처리

Apache Beam에 대해 아시나요? 기존 하둡과 어떤 차이가 있을까요?
좋게 만들어진 MapReduce는 어떤 프로그램일까요? 데이터의 Size 변화의 관점에서 설명할 수 있을까요?
여러 MR작업의 연쇄로 최종결과물이 나올때, 중간에 작업이 Fail날수 있습니다. 작업의 Fail은 어떻게 모니터링 하시겠습니까? 작업들간의 dependency는 어떻게 해결하시겠습니까?
분산환경의 JOIN은, 보통 디스크, CPU, 네트워크 중 어디에서 병목이 발생할까요? 이를 해결하기 위해 무엇을 해야 할까요?
암달의 법칙에 대해 말해봅시다. 그러므로 왜 shared-nothing 구조로 만들어야 하는지 설명해봅시다.
shared-nothing 구조의 단점도 있습니다. 어떤 것이 해당할까요?
Spark이 Hadoop보다 빠른 이유를 I/O 최적화 관점에서 생각해봅시다.
카산드라는 망한것 같습니다. 왜 망한것 같나요? 그래도 활용처가 있다면 어디인것 같나요.
TB 단위 이상의 기존 데이터와 시간당 GB단위의 신생 로그가 들어오는 서비스에서 모든 가입자에게 개별적으로 계산된 실시간 서비스(웹)를 제공하기 위한 시스템 구조를 구상해봅시다.
대용량 자료를 빠르게 lookup해야 하는 일이 있습니다. (100GB 이상, 100ms언더로 특정자료 찾기). 어떤 백엔드를 사용하시겠나요? 느린 백엔드를 사용한다면 이를 보완할 방법은 뭐가 있을까요?
데이터를 여러 머신으로 부터 모으기 위해 여러 선택지가 있을 수 있습니다. (flume, fluentd등) 아예 소스로부터 kafka등의 메시징 시스템을 바로 쓸 수도 있습니다. 어떤 것을 선호하시나요? 왜죠?

DeepAR

- Amazon 에서 2017년도에 낸 논문

- RNN network를 기반으로 Autoregressive하게 TimeSeries Data를 예측하는 모델

- 상품의 수요 예측 for Amazon

- ARIMA 같은 기존의 모델은 big data, high dimensional data에 대해서 잘 예측을 수행할 수 없다.

- LSTM output 단에서 mean 과 std 를 추론하는 Dense 를 붙여서 softplus (std) 를 거친 후 Distribution에게 전달하여 confidence level과 함께 sampling 하는 모델

- train 시에는 x_{t-1}대신 true 값의 true_{t-1} 사용하여 속도를 증가, inference 시에는 auto-regressive 형태에 맞게 이전 LSTM cell의 hidden output을 사용

Transformer

Distribution Sampling & Seqeunce to Sequence

Normalizing Flow

- 기본 아이디어 : simple probability distribution으로부터 complex probability distribution을 만들어 내는 것.

- 과정

z 는 확률 변수로써 우리가 알고있는 normal distribution 같은 간단한 확률 분포로 부터 샘플 된 것
x 는 f 함수를 거쳐 나온 확률 변수로 f 는 invertible function (bijective function)들의 composition of sequence 의 결과
x 에서 f 함수를 거쳐 나온 z 는 one-one mapping이 됨 (f_i 들이 invertible이므로 f도 invertible)

4. 여기서 Change of variables formula가 적용이됨.

- f : invertible 이며 동시에 differentiable 한 함수 f, mapping Z domain을 X로 만듦

이때, 위 함수 f를 통해서 Z 의 density (P(z)) 를 사용해서 X의 density를 추론할 수 있다

즉, P(x) 를 P(z)와 f를 사용해서 구할 수 있다는 것을 의미

5. 위의 수식에서 초록색 부분 Jacobian의 determinant는 어떤 space에서의 contract 혹은 expand 정도를 의미함.

하지만 이러한 transformation의 결과에 의해서 z -> x 시에 one-one mapping이므로 상대적 관계는 유지되는 것.

6. normalizing flow는 change of variables의 연속적인 composition of sequence의 결과로 complex distribution 을 만들어 내는 것

References

[1] https://kejdev.github.io/posts/sampling-resampling/

[2] https://colab.research.google.com/github/datascienceschool/book/blob/master/ds/02%20mathematics/08.07%20%EB%B2%A0%ED%83%80%EB%B6%84%ED%8F%AC,%20%EA%B0%90%EB%A7%88%EB%B6%84%ED%8F%AC,%20%EB%94%94%EB%A6%AC%ED%81%B4%EB%A0%88%20%EB%B6%84%ED%8F%AC.ipynb#scrollTo=XRFuCAdT3ydW

[3] https://www.youtube.com/watch?v=i7LjDvsLWCg

ML_MJSHIN