ML 모델을 연구하고 실제 프로덕트 개발을 위해서 모델링을 하는 과정에서 퍼포먼스 향상을 위해 아키텍쳐 서치를 굉장히 많이하게 됩니다. 최근 Diffusion Model을 기반으로 ML 프로덕트를 만드는 경험을 하였는데, 실제로 UNet 기반의 아키텍쳐에서 activation function은 생각보다 중요하게 퍼포먼스에 영향을 주게 되었습니다. (Normalization 방법도..!)
이번 포스팅에서는 이런 중요한 activation function에 대해서 정리하는 시간을 가져보려고 합니다. 저는 주로 제가 공부한 걸 정리하고 나중에 끄집어 내기 위해서 글을 쓰는 편인데, 누군가 검색하였을 때 keyword라도 던져서 도움이 될 수 있기를 바라며 글을 씁니다!
# 간단히

ML 모델을 학습한다는 것의 목적은 non-linearly 하게만 분리할 수 있는 input feature 를 여러 layer를 쌓아 올린 ML 모델을 거쳐서. linearly 하게 분리할 수 있는 feature space 로 변환하고 쉽게 분리될 수 있는 linear한 영역에서 feature를 기반으로 원하는 결과값을 추론할 수 있도록 하는 것입니다. (위 그림처럼!)
이때 layer 들을 쌓는 과정에서 activation function이 매우 중요한 역할을 수행하게 됩니다. W*X + B 를 수행하는 DNN 을 activation 없이 쌓는다면 fₙ(fₙ₋₁(….f₁(x)) 는 결국 f(x) 하나와 동일해진다는 사실은 모두 아실 거라 생각합니다. 그러면 같은 의미로 activation functiondms optimization 과정에서 생성되는 loss landscape에 non-linear curvature 를 더해간다고 어렵게 설명할 수도 있습니다.... 허허
이를 위해서 다양한 activation function들이 연구되어서 사용되고 있지만 아무렇게나 만드는게 아니라 몇가지 중요한 특징을 고려하고 있습니다.
1) non-linearity in optimization landscape (non-linearity 추가)
2) not increase computational complexity of ML model (연산의 부담 증가없이)
3) not hampler the gradient flow during training (학습 과정에서 gradient가 흐를 수 있도록)
4) retain the distribution of data (data의 distribution을 유지)
위의 특징들을 유지하면서 연구된 많은 activation function들이 있고 그 중에서도 자주 사용되는 activation function들에 대해서 이제 알아보도록 하겠습니다.
# 자세히

가장 오랫동안 사용된 activation function의 대표는 Sigmoid 와 Tanh 입니다.

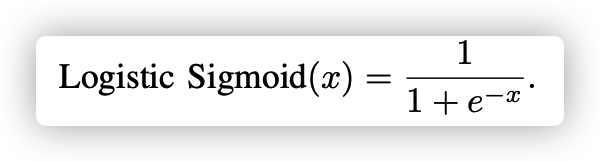
Sigmoid는 0~1 값의 출력값을 가집니다. 가장 큰 특징으로는 input 의 값이 점점 커지거나, 작아질수록 saturation 되는 특징을 가지고 있습니다. 그러나, Sigmoid는 2가지 큰 단점을 가지고 있습니다.
1) 위의 saturation에 의해서 vanishing gradient 문제를 만듦.
2) zero-centric 하지 않은 output을 만들어 내어 convergence에 방해가 됨.
그래서, TanH가 2)의 특징을 해결하면서 사용이 되었습니다. -1 ~ 1 값으로 sturatoin 되는 특징을 가지고 있으면서 output이 0을 중심으로 생성이 되기 때문에 convergence 에서는 조금 더 나을 수 있었습니다. (항상 나은 것은 아닙니다)
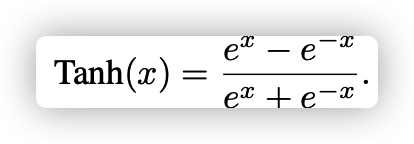
그러나, 역시나 1)의 특징으로 인해서 graident vanishing 문제가 여전히 존재하였습니다. 그리고 은근히 이 두가지 activation은 연산 복잡도가 높았습니다 ...
ReLU는 연산의 단순함과 Performance의 향상, 그리고 saturation이 없는 형태로 많은 인기를 얻었습니다. 그러나, 다음과 같은 3가지 특징이 단점으로 해결하기 위한 연구들이 이루어졌습니다.
1) non-utilization of negative values (음수 Input 영역을 0으로 바꿔버리는 ...)
2) limited non-linearity (linearity가 항상 되는게 아님 ...)
3) unbounded output (한없이 커지는 값 ...)
이때, 1) 의 특징은 vanishing gradient 를 다시 만들어내는 단점이 있었습니다. 그래서 새로운 activation들에 대한 연구가 필요해졌습니다.
그래서 등장한 것이 ELU (Exponential Linear Unit) 입니다. 아래 그림에서 처럼 음수 영역에 대한 input을 0의 값으로 없애버리지 않습니다.

이후에는 Sigmoid, TanH, ReLU, ELU 등이 데이터의 복잡성을 충분히 고려하지 않기 때문에 생기는 문제를 해결하기 위해서 APL (Adaptive Piecewise Linear) 과 Swish 등의 activation function이 등장하게 됩니다. 그리고, Softplus 같은 것들도 등장을 하게 되는데 하나하나 천천히 살펴보도록 하겠습니다.
# 더 자세히

앞에서 언급한 activation functions 들에 대해서 간단히 정리하면 위와 같습니다. Gradient Vanishing 문제를 일으키는 Sigmoid, TanH, ReLU (부분적으로...!) 가 정리되어있고 언급드린 문제들에 대해서 시각적으로 정리가 잘 되어있습니다. [2] 번 reference 논문을 자세히 보시면 도움이 될 거라고 생각합니다 (이 포스팅에서는 이 논문을 기반으로 정리하고 있습니다.)
Sigmoid와 TanH의 문제인 vanishing gradient문제를 해결하기 위해서 sTanh, PSF, ReSech등의 Tanh와 Sigmoid를 기반으로 하는 많은 activation들이 연구되었습니다. 그러나 여전히 saturation 으로 인한 문제는 발생하고 있었습니다. 그래도 그 중에서 가장 많이 사용되는 activation은 Sigmoid-Weighted Linear Unit (SiLU) 입니다. 여전히 문제는 가지고 있지만 자주 사용되는 것이니 수식은 살포시 적어두겠습니다.

ReLU도 역시나 여러 연구가 진행되었습니다. 가장 큰 특징은 negative input에 대해서는 0으로, positive input에 대해서는 identity 역할을 수행한다는 것이고, 이로 인해서 gradient가 0과 1이된다는 점입니다. 그리고 computation 역시 매우 쉽게 이루어진다는 장점이 있어 많이 사용되고 있습니다. 그러나, negative input 영역에서 vanishing gradient문제가 발생한다는 점이 큰 단점입니다. ReLU의 포인트는 negative input 영역에서의 vanishing gradient입니다.
그래서, leaky ReLU 라는 많은 분들이 들어보셨을 법한 activation function이 등장하게 됩니다. 단순하게 컨셉은 이 negative value에 값을 주는 것입니다.

그러나, 위 수식의 0.01인 hyperparameter가 application과 network에 따라서 적합한 값이 다르기 때문에 다소 단점이 있습니다. 이 부분을 해결하기 위해서 PReLU가 등장하여 trainable parameter로 만들었지만, 학습시에 쉽게 overfitting이 일어나서 test 시에 성능을 떨어뜨리는 문제가 존재하여 자주 사용되지는 않습니다. 결국 ReLU가 제일 무난합니다.

이처럼 ReLU는 negative input에 대한 사용을 제대로 못한다는 단점과 함께, 0부근에서 network의 값들이 아주 작은 변화를 가지면서 미세하게 분포되어 있다면 ReLU를 사용했을때 학습이 제대로 안되는 일이 발생합니다. (0.01, -0.005, 0.0003, ... 이런 값들이 ReLU로 들어가는 input을 만들어내는 layer의 ouput이라면 제대로 된 학습이 어려울 수 있습니다.)
ReLU의 단점은 negative input에 대한 처리 방식으로 graident vanishing, unbounded problem 이 있었습니다. unbounded 는 positive input 값이 계속 커지면 무한히 증가하는 ReLU의 특징으로 인해 생겨나며 학습의 불안정성을 발생시키게 됩니다. 그래서 BReLU가 등장했는데 거의 사용은 되지 않고 있습니다.

이런 ReLU 계열의 단점들을 해결하기 위해 등장한게 Exponential Activation 계열입니다. 대표적으로 ELU가 있습니다.

여기서 alpha는 learnable parameter로 application과 network에 맞게 스스로 학습이 가능하도록 하며, larger negative input에 대해서 saturate 하는 것을 통해 noise 에 robustness를 추가해주는 아주 좋은 activation입니다. 논문에서도 ReLU의 장점들을 모두다 가지고 있는 좋은 activation이라고 언급하고 있습니다.
최근에 Diffusion Model에서도 사용되는 Swish는 Learning/Adaptive 계열의 AF입니다. 대표적으로 Swish와 APL이 있습니다.

APL은 a와 b가 trainable parameter 입니다. S는 hyperparameter로 아래와 같이 S값이 hinge loss 형태에서 몇개의 hinges가 생성될 지 정해줄 수 있습니다.

최근 저도 많이 사용하는 Swish는 다음과 같이 표현됩니다.

beta가 trainable parameter 입니다. 이 beta 값은 Swish에서 매우 중요한 역할을 합니다.

위에서 볼 수 있듯이 beta 값에 따라 다양한 형태의 actiavtion function으로 진화하게 됩니다.
마지막으로 설명드릴 두가지 AF는 Softplus와 Mish입니다. Softplus는 아래와 같은 모양을 갖고 있습니다.


Softplus는 diffentiable 한 특징을 가지고 있는 smooth한 형태의 AF로 2001년 논문의 등장과 함께 많이 사용되었습니다. Transformer 를 구현할 때 사용하기도 했었습니다 (저는...).
최근에는 Softplus보다 Mish가 더 자주 사용되는데 아래와 같이 생겼습니다.

가장 큰 Mish의 특징은 non-monotonic 이라는 것이며 softplus처럼 smooth 하다는 것입니다. 최근에는 Yolo v4에서 object detction을 위해서 사용되었습니다.

하지만 연산의 복잡성이 증가하여 사용에 단점이 있다고 합니다. computation은 소중하죠 ..!
# 정리
이렇게 다양한 AF들이 존재하고 있지만 실제로 많은 구현체들은 하나만 쓰기보다 각자 모델과 응용에 따라 쓰고 있습니다. 논문에서도

ReLU, SeLU, Mish, APL이 각각 다른 응용에서 성능이 각자 잘나왔다고 언급하고 있기 때문에 ML product 개발 시에 activation 까지 서칭해주는게 성능을 마지막에 끌어올리기 위해서 좋은 방법 중 하나가 될 것이라고 생각합니다!
References
'ML' 카테고리의 다른 글
| Parameter Efficient Fine-Tuning(PEFT) (0) | 2024.01.18 |
|---|---|
| [Optimization] Gradient Descent, Stocastic Gradient Descent, NAG, RMSPro, Adam (0) | 2022.06.15 |
| [Normalization Techniques] 2탄 Decomposing Normalization (0) | 2022.05.30 |
| [Normalization Techniques] (0) | 2022.05.30 |
| [GluonCV, OpenSource 분석하기] GluonCV의 multiprocessing 이해하기 [2] (0) | 2021.10.27 |



