[ML] Rejection Sampling
잡담
오늘은 Distribution Fit에 대해서 오랜만에 글을 정리해보려고 합니다. ML 내용은 아니지만 최근 MLOps 스터디와 여러 프로젝트들을 수행하면서 모델 적 접근도 중요하지만 Data의 정제와 분석이 훨씬 더 중요하다는 생각이 들어서 이런 공부를 더 많이하는 것 같습니다.

최근 Coursera에서 Andrew Ng 교수님의 ML Ops 강의를 PseudoLab 분들과 함께 공부하고 있는데 회사에서 겪는 일들에 대해서 다시한번 개념적 정의를 할 수도 있고 "모델 < 데이터" 의 중요도에 대해서 느끼고 있던 차에 강의에서도 다시 짚어줘서 재밌는 경험을 하고 있습니다.
위는 ML Ops의 cyclic process 에 대한 그림인데 Data 와 관련된 분석 이후에는 모든 단계에서 Data로 다시 돌아가는 걸 볼 수 있습니다. 그만큼 데이터가 ML 에서는 중요하다!
Introduction

시계열 데이터를 위해서 저는 공부를 했기때문에 시계열 데이터를 기준으로 이야기를 하게 될 것 같습니다. 우선, 시계열 데이터는 시간에 따라 정렬된 일련의 관측값 이라고 정의를 내릴 수 있습니다.
그리고 대표적인 시계열 데이터하면 위와 같은 형태로 익숙합니다.
그러나 딱 위와 같은 하나의 형태로 된 데이터만이 시계열은 아닙니다. 아래와 같이 다양한 특징들을 가질 수 있으며, 다른 타임 스텝 (시간)에 측정된 어떤 측정 값들의 연속된 형태로 정렬한 데이터라면 시계열로 볼 수 있습니다.
- cotinuous vs discrete
- univariate vs multivariate
- evenly sampled vs unevenly sampled
- periodic vs a periodic
- stationary vs nonstationary
- short vs long
- …
이때, 시계열 데이터에서 확률 분포 (probability distribution)는 시간 내에서 관측된 값이 특정 값의 범위에 떨어질 확률을 나타내게 됩니다.
많은 시계열 분포에 대한 분석을 할 떄에는 대부분 시계열 샘플들이 특정 population probability distribution에서 나왔다고 가정을 하며 normal distribution을 가정합니다.
“population” : a population is the entire collection of objects of interest.
그럼 왜 이런 가정을 하는 것 일까요? 그 이유는 저희가 "통계적 사고"를 사용하여 시계열의 샘플 데이터를 분석하여 poluation에 대한 추론을 이끌어낼 수 있습니다. 즉, 가지고 있는 시계열 관측 값들 전체에 대한 어떤 특징을 이해하고 예측할 수 있게 되기 때문입니다.
특히, 우리는 샘플 데이터에 맞는 모델의 개념 (실제 세계의 수학적 추상화라고 표현 하는 .....)을 사용합니다. 저희가 가정한 distribution model이 우리가 관측하여 가지고 있는 데이터 셋에 대해서 잘 fit되어 있다면, 즉 데이터가 변화하고 생성되는 방식을 잘 근사할 수 있다면 population 모집단의 행동도 근사할 수 있다고 가정하게 됩니다.
이러면 ML 모델 학습에 필요한 data augmentation이나 여러가지 모델의 성능을 증가시키기 위한 방법이 많아지게 되고 강력한 모델을 만들어 낼 수 있게 됩니다.
문제는, 시계열 데이터들은 대부분 데이터가 inertia 나 carry over 때문에 autocorrelation이 발생하여서 sample size가 적은 경우 제대로 된 distribution fit같은게 어려워 지는 문제점이 있습니다. 추후에 기회가 되면 다루어보겠습니다! 혹시 알아보고 싶으신 분들은 아래의 키워드로 공부해보시면 될 것 같습니다.
- autocorrelation
- serial correlation
- lagged correlation
- persistence
Distribution Fit
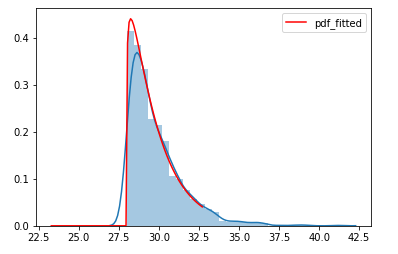
파란색 : 관측 시계열 데이터, skewed normal로 fit을 하게되면 데이터를 잘 fit할 수 있는 예
Distribution Fitting 은 데이터에 가장 적합한 distribution 을 알아내는 방법입니다. 이러한 방법을 통해 관측된 데이터를 기반으로 통계학적 정보를 사용하고자 할 때 해당 fit된 distribution을 사용하여 조금 과장을 보태면 모든 것을 대체할 수 있게됩니다.
보통 distribution fitting을 수행할 때는 다음과 같은 4가지의 parameter들을 사용하여 적합한 distribution을 찾습니다.
- location
- scale
- shape
- threshold
모든 distribution이 위의 4가지 parameter를 가지고 있는 것은 아니고 다른 parameter들을 요구하기도 합니다. 예를 들면 normal distribution은 2개 scale (std)과 location (평균) 만을 사용합니다.


가장 쉬운 예시로 location이 변하면 평균의 위치가 변합니다. 그리고 Scale이 변하면 데이터의 퍼짐 정도가 다르게 되기 때문에 아래 그림과 같이 변합니다.
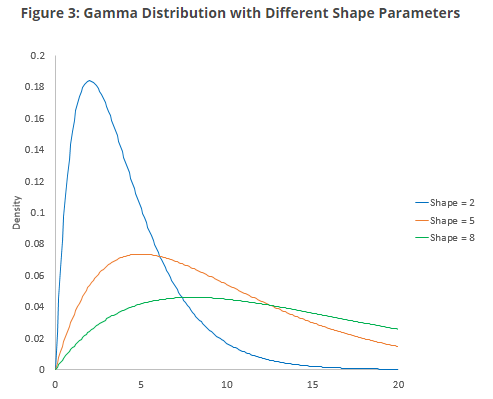
반면 Shape는 조금 다르게 변화합니다. normal distribution이 skewed normal distribution으로 변하는 것을 볼 수 있습니다. 보통 shape parameter가 클수록 분포가 왼쪽으로 치우치는 경향이 있습니다. 반면 shape parameter가 작을수록 분포가 오른쪽으로 치우치는 경향이 있습니다.
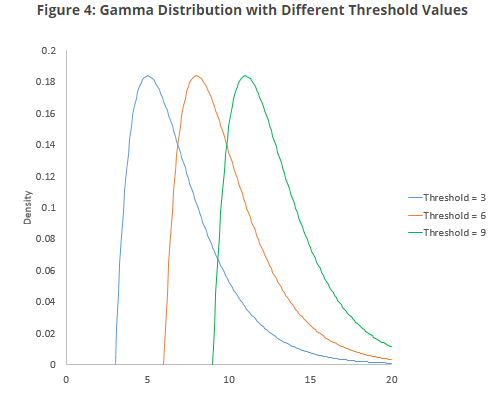
그리고 마지막으로, 분포의 threshold parameter는 x축을 따라 분포의 최소값을 정의합니다. 분포는 이 threshold parameter 미만의 영역에서 어떤 확률도 가지지 않아 데이터가 발생하지 않습니다.
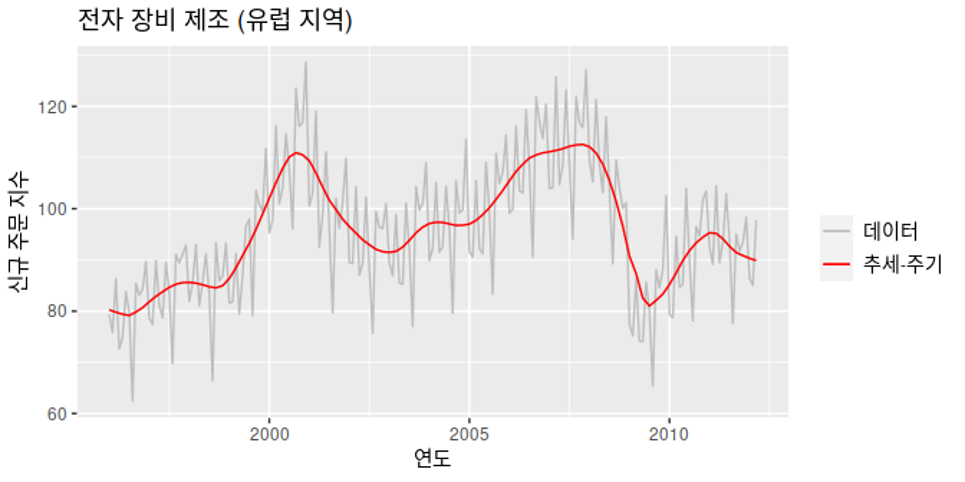
전자 장비 신규 주문 지수 (https://otexts.com/fppkr/components.html)
그러면, 시계열 데이터에서 distribution fit을 어떻게 사용할지에 대해서 살짝 알아보도록 하겠습니다. 위와 같은 시계열 데이터가 존재한다고 가정하고 저희는 cycle이 있어보이는 2000 ~ 2005년, 2005~2010년 과 같이 5년 단위의 시계열을 구간으로 나눈 뒤 2.5년 단위로 fit을 진행할 수 있겠죠.
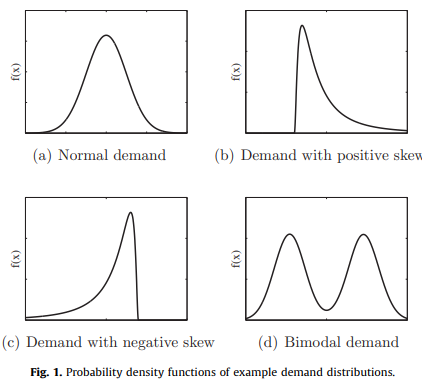
그리고 보통 이런 시계열은 위와 같이 4개의 distribution 형태를 따른다고 가정하고 있기 때문에, 이 중 하나로 fit이 되게됩니다. parameter는 튜닝이 필요하지만 위의 형태 중 하나로 fit이 가능해지며, 이를 사용해서 저희는 새로운 데이터를 생성해 낼 수 있게됩니다.
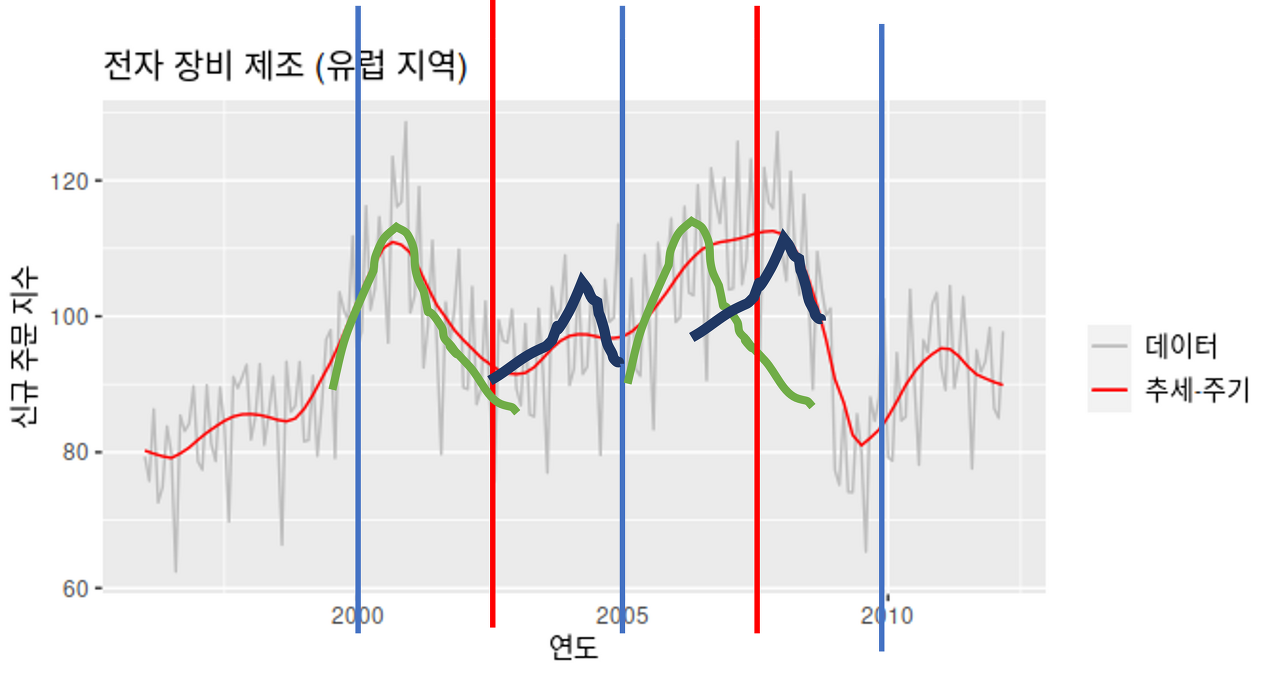
제가 그림을 매우매우 못그렸지만, 초록색의 positive skew와 파란색의 negative skew가 반복되는 듯한 형태로 distribution이 2.5년 주기로 fit하면 어느정도 시계열 데이터의 분석이 가능해 지는 것을 볼 수 있습니다.
그리고 이를 사용해서 ML model의 학습을 위해 data를 augmentation을 한다고 하면 fitting된 distribution을 가지고 새로운 시계열 데이터를 sampling해서 모델의 성능을 향상시킬 수 있게 되는거죠.
Rejection Sampling
저희는 가진 data 로부터 유사 확률분포를 얻을 수 있게 되었기 때문에 sampling을 통해 data augmentation을 이뤄낼 수 있습니다.
이 방법으로 rejection sampling이라는 방법이 있습니다. 우선, rejection sampling의 개념부터 알아보겠습니다.
Rejection sampling은 우리가 가질 수 있는 확률 분포에서 효율적으로 샘플을 생성하기 위한 알고리즘입니다. 위에서 저희는 data 로 부터 distribution fit을 통해서 유사 확률 분포의 pdf를 얻었습니다.
그러나, 위의 유사 확률 분포는 복잡하여 샘플링을 하기 어렵다고 생각해보겠습니다. 그리고 이런 어려운 확률 분포를 로 정의하겠습니다. 그리고, 저희는 normal distribution 이라는 매우 쉽게 샘플링 할 수 있는 확률 분포 를 알고 있습니다.
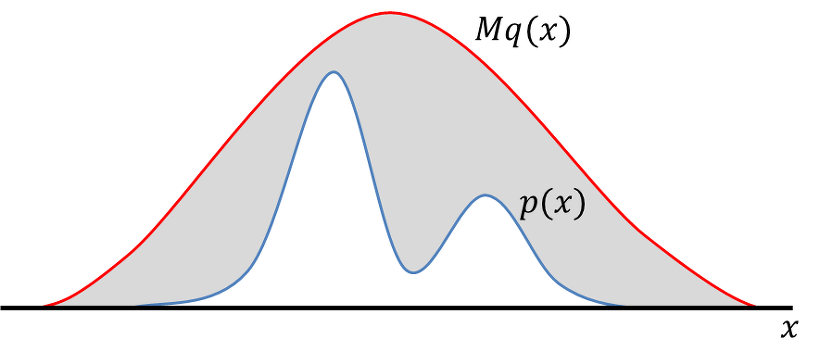
확률 분포 , 와 상수 M (https://untitledtblog.tistory.com/134)
이때, 상수 M이 등장을 하게 됩니다. 상수 M은 우리가 정의한 유사 확률 분포 에서 확률 변수 x가 값을 취할 수 있는 모든 x 에 대해 p(x)<=M*q(x)가 되도록 하는 상수입니다.
쉽게 생각하자면, 분포는 x 가 1, 2, 3 그리고 5에서 만 값을 갖으며 각각 의 확률을 갖는다고 가정해보겠습니다.
그리고, 쉬운 확률 분포의 해당 x 에서의 확률이 이라고 한다면 저희는 M=3 을 선택할 수 있게 됩니다. 만약 이라면, 확률 변수 x 에서 는 가 되어 위의 조건 을 만족한다는 것을 알 수 있습니다.
이렇게 M을 정의한 후에는 매우 간단하게 샘플링을 할 수 있게 됩니다.
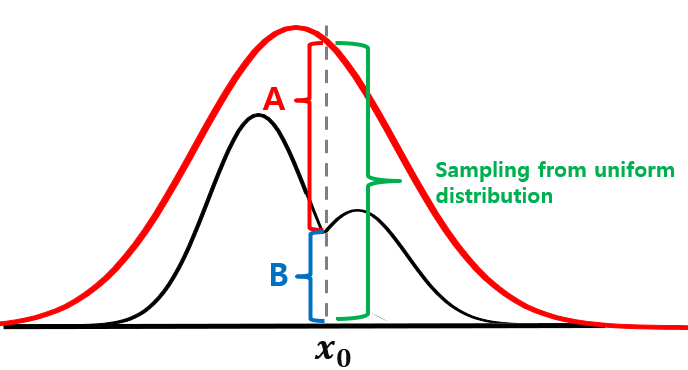
uniform distribution으로 부터 하나의 값 을 샘플링 합니다. 그리고, 의 값이 B 구간에 속하는 값이라면 해당 x0 의 확률 변수를 샘플링 합니다.
위의 방법은 기본적인 rejection sampling 으로 샘플을 샘플링 하는 방법입니다. 그러나, 이 포스트에서 설명하고자 하는 시계열 augmentation으로는 어떻게 사용할 수 있을까요? 그 방법은 다음과 같습니다.
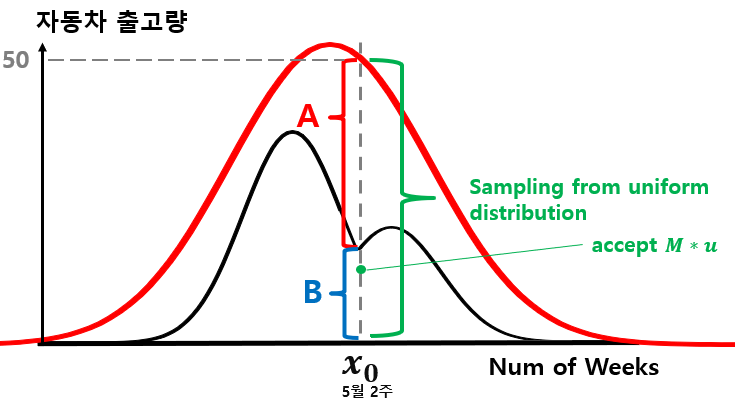
uniform sampling으로 값 를 가져온 후, u 값이 만약 A or B 구간에 속한다면 그 값을 time x_0의 샘플로 사용하는 것입니다. 위와 같은 방법은 시계열로부터 distribution fit을 수행하고 이렇게 얻게 된 유사 확률 분포를 이용해서 데이터를 augmentation 할 수 있는 하나의 방법이 될 수 있습니다.
이번 포스팅에서는 시계열을 augmentation 할 수 있는 하나의 방법을 소개했습니다. 저도 공부하면서 남기는 블로그라서 글이 어지럽지만 도움이 되었으면 합니다!
Reference
- http://incredible.ai/statistics/2015/06/13/Distribution-Estimation/
- https://imedea.uib-csic.es/master/cambioglobal/Modulo_V_cod101615/Theory/TSA_theory_part1.pdf
- http://incredible.ai/statistics/2015/06/13/Distribution-Estimation/
- https://www.spcforexcel.com/knowledge/basic-statistics/distribution-fitting
- https://www.researchgate.net/publication/275286645_Impact_of_the_shape_of_demand_distribution_in_decision_models_for_operations_management
- https://untitledtblog.tistory.com/134