[Optimization] Gradient Descent, Stocastic Gradient Descent, NAG, RMSPro, Adam
1) Gradient Descent
parameter 를 반복적으로 objective 의 gradient 를 이용해서 update 하는 방법. 주어진 데이터 D를 사용해서 objective 가 optimal value에 도달할 수 있도록 점진적으로 update를 수행.
(ex) Linear regression

Step 1. objective L(theta) 를 parameter theta에 대해서 미분을 수행

Step 2. theta 를 gradient 의 반대 방향으로 update. (f_theta = th_1 * x_1 + th_2 * x_2 + ... + th_j * x_j + ... + th_N * x_N 이므로 뒤에 x_j가 남게됨)

그러나, Gradient Descent 방법은 N 개의 샘플이 D 차원을 가지고 있을 때 O(ND)의 computation complexity를 가짐.
2) Stochastic Gradient Descent
SGD는 기본적으로 1개의 sample만을 가지고 gradient를 계산해서 parameter를 업데이트 하는 방법을 의미. 위의 GD 처럼 주어진 모든 샘플을 가지고 gradient 를 정확히 계산하는 방법이 아님. 한번에 계산해야하는 gradient 의 sample 이 1개이므로 computation complexity 가 O(D)로 줄어듦.

위의 Linear regression 문제를 예시로 들면, 아래와 같이 업데이트시에 sample이 1개만 고려됨.

논문에서는 샘플 수 N이 클 때, 이렇게 줄어드는 computation complexity가 iteration 증가에 따른 computation complexity보다 효율적이라고 언급.

GD는 항상 optimal value를 계산해서 gradient의 negative direction으로 parameter를 업데이트하지만, SGD는 1개의 sample 만을 가지고 gradient 를 계산하기 때문에 매 샘플이 가지는 gradient의 variance 가 크기 때문에 update가 불안정 (oscillate)하게 이루어짐. 그래서, GD와 SGD를 결합해서 만든 것이 Mini-batch gradient descent method (MSGD)이며 우리가 흔히 pytorch나 tensorflow를 통해서 학습할 때 사용하는 방법이 MSGD 입니다.
3) Mini-Batch Gradient Descent (MSGD)
GD처럼 항상 optimal graident value를 찾는 경우 현재 parameter가 objective surface의 local minima 에 빠져있는경우 gradient 값이 계속 0과 유사한 값이 나오면서 업데이트가 이루어지지 않을 가능성이 높음. 그러나, MSGD의 경우 randomly smapled 데이터 mini-batch 단위로 업데이트를 수행하므로 gradient가 stochastic 한 noise 를 가지게 되어 local minima를 탈출할 수 있는 가능성을 제공함. (MSGD의 'stochastic'은 매 배치를 구성하는 sample이 랜덤하게 선택되었음을 의미하는 단어)
MSGD를 사용하여도 multi-modal 문제에서 수많은 objectice surface가 가지는 local minima를 탈출하도록 하는 것이 중요한 문제이며, 실제로는 local minima 보다 saddle point가 더 큰 문제라는 연구 결과가 있음. (고차원의 공간에서 모든 축의 방향으로 오목한 형태가 형성될 확률은 거의 0에 가깝다는게 주장. local minimum이라면 모든 변수 방향에서 loss가 증가해야 하는데, 이런 경우는 흔치 않기 때문.)
Saddle Point란 Saddle point 지점뿐만 아니라 그 주변 언저리는 평평하기 때문에 굉장히 더디게 학습이 진행되며 gradient도 0에 가까워 optimal direction을 찾기가 어려운 지점을 의미.

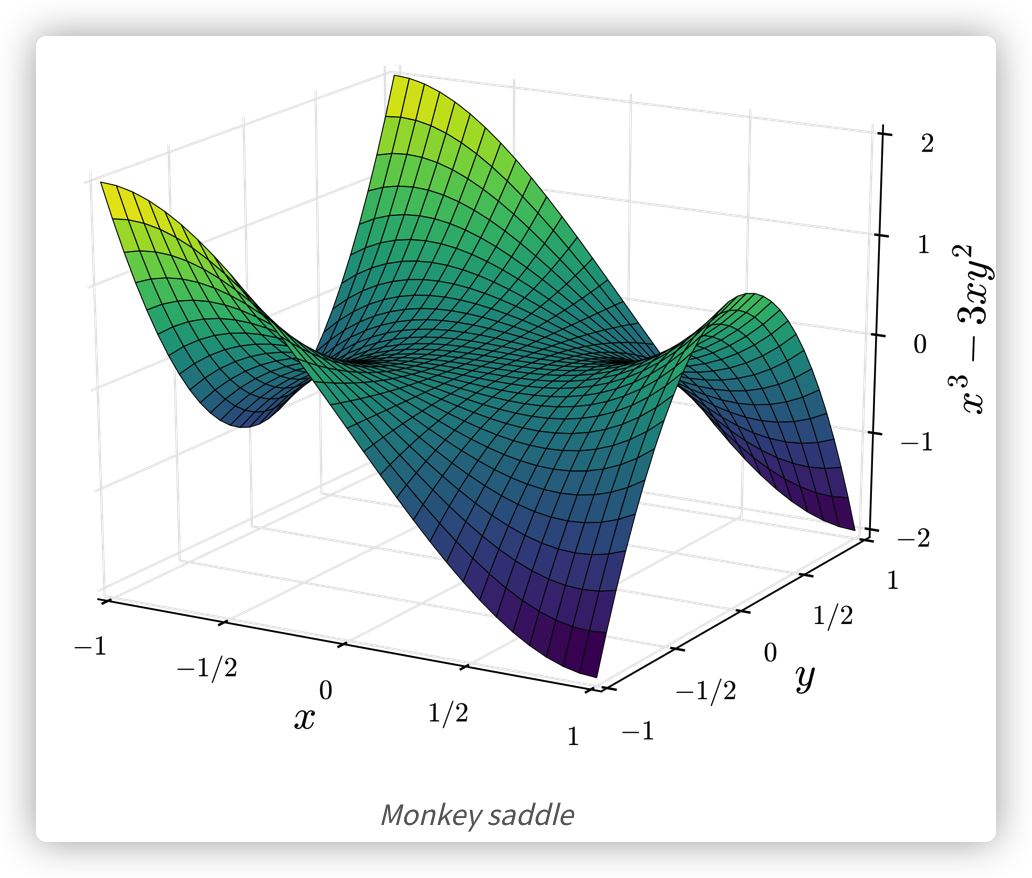
# 자세히
- Nesterov Accelerated Gradient Descent (NAG)
physics 의 관성의 개념을 가져와서 SGD를 향상시킨 optimization 알고리즘.

NAG를 이해하기 위해서는 Momentum 기반 GD에 대한 기초적인 이해가 필요합니다. 위의 수식이 momentum 알고리즘의 수식입니다. g(theta_t)는 현재 t 에서의 gradient값을 의미합니다. v_t는 speed를 나타내는 계수이며 e 는 learning rate for momentum, mu 는 기존 speed에 대한 반영 계수 입니다. 위의 계수들을 통해서 계산된 v 가 parameter theta를 업데이트 할 때 더해지는 방식이 momentum 알고리즘의 parameter optimization 방법입니다.

이 momentum 알고리즘을 통한 parameter update 방법을 그림으로 표현하면 위와 같습니다. 이 방법의 장점은 아래 그림과 같이 이전 학습에서 업데이트 된 gradient 의 방향성을 다음 업데이트에 반영하게 되면서 stochastic gradient descent 가 가질 수 있는 batch 로 인한 gradient 의 variance로 인해 생기는 oscillate를 줄여줄 수 있게 됩니다.

NAG의 수식은 위의 momentum 알고리즘과 아주 약간만 다릅니다.

유일한 차이점은 gradient 를 구할 때 현재의 parameter theta_t 에서 구하는 것이 아니라, 가지고 있는 momentum v만큼을 theta_t에 더해준 뒤 new_theta를 기준으로 gradient를 계산한 다음 momentum에 더해주는 방식입니다.

이렇게 구한 gradient g(theta_t - mu * v_t) 는 g(theta_t)와 다른 값을 가지게 되고 업데이트 된 theta_(t+1)도 다른 값을 가지게 됩니다. 실제 구현을 위해서는 theta_t - mu * v_t 에서의 gradient 를 구하는 것의 복잡성 때문에 여러 트릭을 통해서 수식을 변형하여 간단한 형태로 구현하고 있습니다.
NAG의 momentum 을 통한 optimization 방식은 local minima를 효과적으로 탈출하고 oscillation을 줄여주어 학습의 수렴을 안정적으로 가능하게 만들어 줍니다. 이때 momentum의 계수들에 대한 조절이 매우 중요한 요소이며 보통 0.9를 모멘텀 factor로써 사용하는게 일반적입니다.
- Adaptive Learning Rate Method
momentum 을 활용하는 방식 이외에 학습의 중요한 요소를 결정 짓는 learning rate를 automatically 조정해주는 방법도 제안되었습니다. 대표적으로 SGD에서 이 방법을 적용시킨 방법이 AdaGrad 입니다. AdaGrad는 이전 parameter update iteration에서의 gradient update history를 사용해서 learning rate를 조절합니다.

gt 는 time t 에서의 parameter θ의 gradient 입니다. Vt는 time 1 부터 t 까지 parameter θ gradient 들의 합 입니다. GD와 AdaGrad의 유일한 차이점은 iteration이 진행됨에 따라서 누적된 gradient 의 합에 의해서 learning rate가 automatic 하게 조정된다는 것 입니다. 단점으로는 여전히 η 계수를 수동으로 설정해줘야 하며 학습이 진행되면서 gradient 의 합은 자연스럽게 증가하고 그 결과 learning rate가 0에 가까워 진다는 것입니다.
이렇게 learning rate가 0이 되어 버리는 문제를 해결하기 위해 등장한 대표적인 방법이 RMSProp(Root Mean Square Prop)입니다. RMSProp은 다음과 같은 특징을 가집니다.
모든 gradient의 history를 더하지 않는다가 포인트입니다. 이와 동시에 momentum 의 개념을 더해서 gradient history를 모두 더하지 않고 t 와 t-1 의 history를 누적으로 이동평균 만들어서 learning rate를 조절하게 됩니다.

위의 사진과 같은 objective surface 가 있다고 가정해보겠습니다. 이때, 2개의 feature dimension w & b가 있다고 가정할 수 있습니다. 이렇게 되면 우리는 각각의 feature 방향에 대한 learning rate를 조절하여 parameter 를 업데이트 할 수 있게 됩니다.

위의 수식의 S가 AdaGrad의 history gradient의 합의 역할을 하고 있습니다. 그런데 이전 기록들의 전체 합이 아니라, 이전 기록과 이번에 계산된 gradient의 제곱의 가중 평균이 사용됩니다. 그리고 parameter를 업데이트 할 때는 AdaGrad와 같은 방법으로 learning rate를 조절해서 업데이트 해주는 방식이 RMSProp 입니다.
Adaptive Moment Estimation (Adam) 도 SGD의 단점을 향상시키며 등장한 optimzation 방법입니다. momentum과 RMSProp의 장점들을 잘 결합하여 만들어져 있습니다.

Momentum에서 관성계수 m을 기반으로 parameter를 업데이트하면서, gradient g의 제곱값의 지수이동평균을 활용하여 learning rate를 조절합니다.